目标:实现一个算法,模拟在一个封闭二维区域,圆形小球朝给定方向坠落的过程,实现二维区域的紧密填充。
像下面这样:

难点,及其简单解决:
1.如何把粒子移动尽可能远?
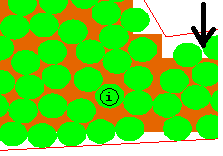
图中的粒子i,能往下移动多远?一般情况,碰撞?边界?
一个简单解法:
注意如下事实:判断两个粒子是否重叠,判断粒子是否和边 界线重叠,都是十分容易的。
据此定义函数 f (r) 如下

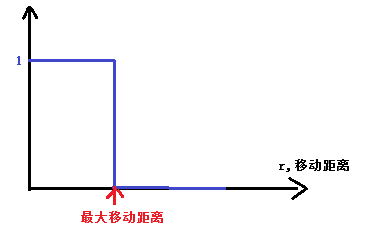
考虑把粒子往前推的过程,最开始 f (r) = 1,当推进到一个临界值后,f (r) = 0,
因此,f (r) 的函数图像是:
代码如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
|
//找出一个点,在一个方向上最远可以前进多远,限于一步之内,该点可以不属于这个mesh,如果不能前进,返回false
bool most_advance(Point* p,double direc_x,double direc_y,Mesh *mesh,double &x,double &y,double &best){
//二分法求根。
if(!(p->can_move))
return false;
double low_radio=0.0;
double high_radio=1.0;//mesh->x_num + mesh->y_num;
best=low_radio;
bool at_least_one_success=false;
double mid;
double step=mesh->get_step();
Point new_point;
while(fabs(low_radio-high_radio)>0.000001){
mid=(low_radio+high_radio)/2;
new_point.x=p->x + direc_x * step * mid;
new_point.y=p->y + direc_y * step * mid;
bool result=mesh->can_move_point(p,new_point);
if(result){
low_radio=mid;
best=max(best,mid);
at_least_one_success=true;
}else{
high_radio=mid;
}
//cout<<"mid="<<mid<<" best="<<best<<" result="<<result<<endl;
}
if(!at_least_one_success)
return false;
x=p->x + direc_x * step * best;
y=p->y + direc_y * step * best;
return true;
}
|



